➡ Click here: Leap year c program
Was the memory allocation successful? DO NOT IMPLEMENT WIKIPEDIA ALGORITHM! AND Second condition will check year % 100 reminder is not equal to 0. CODE Let us check for normal year Not Leap Year ANALYSIS Since we have to check multiple conditions within one If Statement, we used Logical AND and Logical OR operators.

Our Founder has trained employees of almost all Top Companies in India such as VMware, Citrix, Oracle, Motorola, Ericsson, Aricent, HP, Intuit, Microsoft, Cisco, SAP Labs, Siemens, Symantec, Redhat, Chelsio, Cavium, ST-Micro, Samsung, LG-Soft, Wipro, TCS, HCL, IBM, Accenture, HSBC, Mphasis, Tata-Elxsi, Tata VSNL, Mindtree, Prime and Startups. There is no way that the tests on the right side of the logical AND can make the outcome true, so nothing else gets evaluated. Yes, in the scheme of things. So the given number is definitely Leap year. Mod 400 and Mod 100 must be social every time, when the Mod 4 term could have ruled those out 75% of the time see my answer above. Take a year as input and store it in the variable year. F only 100 divides year. But when the user doesn't want to enter another met, the program will then display all the years entered and will write if the year is leap or not. Granted, this is not a leap year c program saving. Many Roman Catholic countries changed in 1584; countries under British sway changed in 1752; other countries changed at different times Russia in the 20th between; the Russian Orthodox church still hasn't changed, AFAIK.
What happens when the user enters more than 10 years? It is very desirable to avoid.
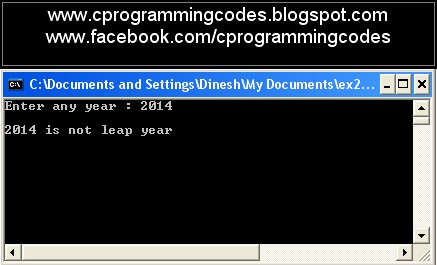
Full Program: - As per the algorithm any number that is divisible by 400 is a Leap year. As per the algorithm any number that is divisible by 4 but not divisible by 100 then that number is Leap Year.

I made a program using C to find whether the entered year is a leap year or not. But unfortunately its not working well. It says a year is leap and the preceding year is not leap. DO NOT IMPLEMENT WIKIPEDIA ALGORITHM! By re-ordering the algorithm to perform the 4th year test first we speed things up significantly. NOTE: I have fought various Wikipedia editors to improve the algorithm published there, arguing that many novice—and professional—programmers quickly arrive at the Wikipedia page due to top search engine listings and implement the Wikipedia pseudo-code without any further research. Wikipedia editors repudiated and deleted every attempt I made to improve, annotate or even merely footnote the published algorithm. Apparently, they feel finding efficiencies is the programmer's problem. That may be true, but many programmers are too hurried to perform solid research! Performing a modulo calculation requires division. One doesn't often think twice about this when programming a PC, but when programming 8-bit microcontrollers embedded in small devices you may find that a divide function cannot be natively performed by the CPU. It is very desirable to avoid. Bitwise-AND is a single instruction on every CPU. There exists no power of two that equals 100. Thus, we are forced to continue to use the modulo operation for the 100th year test, however 100 is replaced by 25 see below. We can do this because 100 factors out to 2 x 2 x 5 x 5. Because the 4th year test already checks for factors of 4 we can eliminate that factor from 100, leaving 25. This optimization is probably insignificant to nearly every CPU implementation as both 100 and 25 fit in 8-bits. Again, we can do this because 400 factors out to 2 x 2 x 2 x 2 x 5 x 5. We can eliminate the factor of 25 which is tested by the 100th year test, leaving 16. We cannot further reduce 16 because 8 is a factor of 200, so removing any more factors would produce a unwanted positive for a 200th year. The 400th year optimization is greatly important to 8-bit CPUs, first, because it avoids division; but, more important, because the value 400 is a 9-bit number which is much more difficult to deal with in an 8-bit CPU. Short-circuit operators are so named because they do not bother to evaluate the expression on the right side if the expression on the left side, by itself, dictates the outcome of the operation. There is no way that the tests on the right side of the logical AND can make the outcome true, so nothing else gets evaluated. By performing the 4th year test first, only the 4th year test a simple bitwise-AND is evaluated three-quarters 75 percent of the time. This speeds up program execution greatly, especially since it avoids the division necessary for the 100th year test the modulo 25 operation. The logical AND operator has higher precedence than logical OR and will be evaluated first with or without the new parentheses. Parentheses around the logical AND arguments has no effect. Thus, a useful optimization has been mistakenly eliminated. The right side of the logical OR is only evaluated for years divisible by 4 and 100 because of the short-circuit OR. Inefficiency, primarily due to the order of execution. Mod 400 and Mod 100 must be calculated every time, when the Mod 4 term could have ruled those out 75% of the time see my answer above. Yes, in the scheme of things. However, when looking for a reference answer, the Wikipedia algorithm is too-often repeated as a good one and it isn't very good at all. I wouldn't call reversing the order of the terms put year % 4 first micro-optimizing, nor would I call the use of modulo especially beginner friendly or readable in the first place. Instead, the weak algorithm on Wikipedia has become canonical and the world stands still. Granted, this is not a huge saving. Rationale: modulus division is slow on some platforms whereas a single bitwise-AND is typically one instruction cycle. Some language compilers perform this optimization automatically, but baking it into the code guarantees it. Technically, % 100 can be replaced with % 25 but this is not likely an improvement for any system. Many Roman Catholic countries changed in 1584; countries under British sway changed in 1752; other countries changed at different times Russia in the 20th century; the Russian Orthodox church still hasn't changed, AFAIK. Check the output from cal 9 1752 on a Unix-ish machine. Also, for negative values of year, you have to wrestle with the presence or absence of a year 0. Negative modulo 4 values i. This doesn't work for one's complement representations. Further complications are pointed out by JonathanLeffler supra. The second part of the rule effects century years. For example; the century years 1600 and 2000 are leap years, but the century years 1700, 1800, and 1900 are not. This means that three times out of every four hundred years there are eight years between leap years. Kevin's answer provides an optimal 8 operation test with XOR using constants but if you are looking for something a bit more readable, try this 9 operation test. F only 100 divides year. T 100 and 400 divides year.

